

The Swinging Blind Juggler achieves stable juggling without any sensors to detect the ball. The same paddle shape and motion that stabilize the ball on the Blind Juggler also keep the ball from falling off the Swinging Blind Juggler. While the ball motion is stable without sensing, we need feedback to control the pendulum motion. Blind juggling is only possible if the pendulum remains synchronized to the ball motion. We developed a feedback strategy that uses special paddle motions to control the pendulum motion. The physics that make this possible are similar to what children intuitively use to control their amplitude on a swing.
Four Bar Linkage
Blind juggling only works if the paddle is perpendicular to the ball velocity at impact (Figure 1: see the red highlights that indicate velocity and paddle alignment in the sketch). Instead of actively rotating the paddle with a motor, we use a mechanism called a „four back linkage“. The four bar linkage passively keeps the paddle perpendicular to the ball velocity at impact.
We obtained the link lengths and trough an optimisation to keeping the paddle perpendicular to ball impact velocity, the optimisation also tried to match the natural period and ball flight time were not matched up, we would need very powerful motors to force the pendulum to swing in phase with the ball.
Feedback Control for the Swinging Blind Juggler
The side-to-side juggling only works if the pendulum is synchronized to the ball motion, i.e. the pendulum has to position the paddle correctly to strike the ball. Previously, we used motors attached at the pivots to synchronize the pendulum to the ball motion. Here, we propose a more elegant way to achieve synchronization by adapting the paddle motion. The key idea is to exploit the dynamic coupling between the motion of the paddle and the pendulum. Children on a swing intuitively use a similar dynamic coupling to control their amplitude. They can swing higher and higher by moving up and down. In a similar way, we want to control the pendulum with appropriate paddle motions.
© Flavio Fontana
For more information about how kids pump a swing, see the work of William Case, for example this paper.
Feedback control using the paddle
The Swinging Blind Juggler measures where the pendulum is at impact. Based on this measurement, the robot selects an appropriate paddle motion that positions the pendulum for the next impact.
We explain how this feedback strategy works with a simplified example (you may also find a video about the feedback strategy below). A sensor located at the top of the pendulum measures the pendulum angle at ball impact. At ball impact, the robot measures the pendulum angle. It may be that the measured angle is different from the ideal angle for striking the ball. For example, the pendulum could swing a bit too far because a spectator pushed the Swinging Blind Juggler a little. Therefore, the robot needs to be able to react to deviations of the measured angle from the ideal angle. This is achieved by applying the right paddle motion for the measured deviation.
Figure 2 illustrates how the Swinging Blind Juggler compensates for two deviations (purple and red) from the ideal angle (teal). The right side of the figure illustrates the paddle motions that bring the Swinging Blind Juggler to the correct position for the next ball impact. Note how the gray part is the same in all three paddle motions. This is the striking motion that the paddle must perform to juggle the ball: we can use only the colored section of the paddle motion to react to deviations.
We precompute many of these compensating paddle motions using tools from optimal control, such as the direct transcription method and the Sparse Nonlinear Optimizer SNOPT. The motions are stored in a lookup table where the robot can find the right motion to apply. If you are interested how we computed the paddle motions you can find the source code below.
Additional Content for the Swinging Blind Juggler
Here you can find the Mathematica Notebook that derives the nonlinear dynamics of the Swinging Blind Juggler. If you are interested in how we computed the paddle motions have a look at the Matlab script.
We used the Sparse Nonlinear Optimizer SNOPT to solve the optimal control problem.
VIDEOS
Video showing the Swinging Blind Juggler starting from rest and ultimately juggling at an amplitude of 25 degrees.
Video showing the feedback strategy that uses the paddle motion to synchronize the pendulum to the ball motion.

The Swinging Blind Juggler
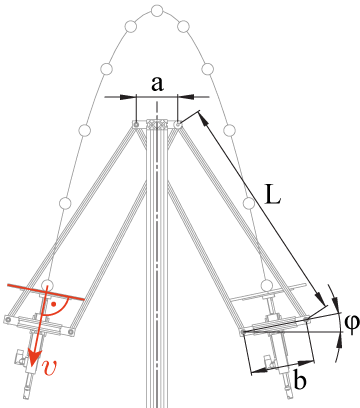
Figure 1
Four bar linkage
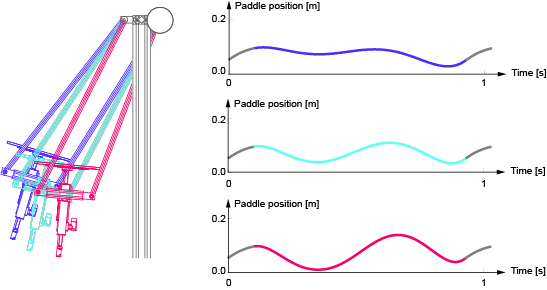
Figure 2
Illustration of paddle motions that compensate for deviations in the pendulum angle.
