
Periodic Orbits
A ball bouncing on an actuated paddle is a nonlinear dynamical system with some fascinating properties. We learn from the analysis of the famous logistic map that nonlinear systems can have periodic orbits. The balls bouncing on the Cloverleaf Blind Juggler can also follow different periodic orbits. This is demonstrated in the following video:
Periodic Orbits
The different periodic orbits shown in the video are visualized in Figure 1 as a plot of ball height versus time.
Local vs. Global Stability
There are different classifications of stability. An important distinction is between local and global stability. The ball orbits are locally stable. That means that as long as the ball stays close to the ideal path along the periodic orbit, the ball stays in that orbit. If the ball deviates too far from the ideal path, however, it will leave the orbit and start moving along another orbit. This is also illustrated in the video above: timing and height are crucial to the resulting orbit when dropping a ball.
In contrast, if one of the ball orbits is globally stable, time and height of a drop do not matter: the ball always ends up in the globally stable orbit. Clearly, if there is a globally stable orbit, there cannot be any other stable orbit.
Basins of Attraction
A map can be created to predict which orbit the ball will follow based on its initial height and velocity at the start of the paddle period (see dashed lines in Figure 2).
Chaos
A ball bouncing on an actuated paddle may seem like a rather simple dynamical system, but it exhibits very rich behavior. For example, the ball motions become chaotic when the paddle motions reach higher frequencies. It is important to note that the paddle motion is deterministic, and not chaotic – only the balls exhibit chaotic behavior. This is illustrated in the following video:
KEY Properties
Two key properties of chaos are well visualized in the video:
- Local instability: Two balls that start very close to each other quickly develop very different motions. This is because small disturbances acting on the balls are amplified by unstable system behavior. There are many possible sources for these small disturbances, such as small breezes of air, differences in the bounciness between balls, or an imperfect paddle surface.
- Strange attractor: Even though the ball behavior is locally unstable, we find that the balls remain within a limited set of positions and velocities when moving chaotically. This set is called the strange attractor of the system. This set is visualized below.
Figure 3 depicts the strange attractor of the chaotic ball motions. Every black dot corresponds to a measured ball height and velocity. The values are measured when the paddle is at the lowest point of the motion that induces chaotic ball motion (see video to watch this paddle motion). The attractive nature of the black set means that if a ball starts outside the black set, for example at the red cross, it quickly converges to the black set. At the same time there is the local instability: if two balls are very close to each other on the black set, they very quickly diverge from each other. This is a key property we use for controlling balls to desired juggling patterns, read more about this here.
VIDEOS
The Cloverleaf Paddle allows the Blind Juggler to juggle up to four balls, showcasing nonlinear system properties. The same paddle motion produces multiple stable ball modes (periodic orbits), as shown at the end.
Video illustrating stable orbits found with the Cloverleaf Blind Juggler.
Video of a first control strategy to automatically generate juggling patterns using chaos.
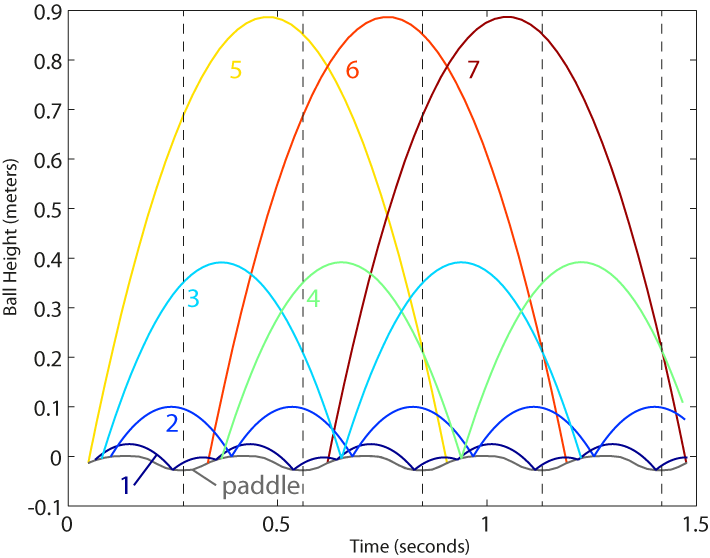
Figure 1
The grey curve is the vertical paddle position and the dashed, vertical lines mark the paddle strokes (periods). There are four distinct orbits: 1, 2, 3, and 5. Orbit 4 is the same as 3, but shifted, and 6 and 7 are the shifted versions of 5. In the video above, we introduce the notation we use for the orbits (we use the notation introduced by T. Heimsch and R. Leine). Number 1 is a orbit, which reads as follows: The ball motion has a period of 1 paddle stroke and there are two impacts per period. The period corresponds to the number of paddle strokes one can count before the ball motion repeats itself. This is best explained in the video above. Another example is orbit 2, which is a orbit: There is one impact and the period is one paddle stroke. Orbits 3 and 4 are , and orbits 5,6,7 are orbits. Lastly, we introduce letters to differentiate between shifted versions of the same orbit: Number 7 is the orbit and refers to orbit 5 and to 6. In total, we find 7 different stable ball motions.

Figure 2
The basins of attraction of the different stable orbits. The map is best explained with an example: In Figure 1, we find that a ball on orbit number 2 (the orbit) is at about 0.1 meters height and slowly falling at the first dashed line. Slowly falling corresponds to a small negative ball velocity. We now look up 0.1 meters ball height and a small, negative velocity in the orbit map (see left arrow). We find that the corresponding area is indeed medium blue, which refers to the orbit. The basin of attraction of the orbit is the collection of all medium blue areas, i.e. all possible heights and velocities that result in the ball following the orbit. The map also predicts less obvious outcomes: If the height is about 1.8 meters and the velocity is slightly negative (right arrow), the ball will end up in the orbit, after a possibly complicated transition (watch the video here for an example of a non-straightforward transition).
The number and the types of orbits we find depend on the specific paddle motion. For example, the paddle motion shown in Figure 1 has a short period at the lowest height where the paddle is at rest. One of the impacts of the orbit occurs in this short period. If we change the paddle motion such that the paddle is not at rest anymore at the lowest height, we do not find the orbit anymore.
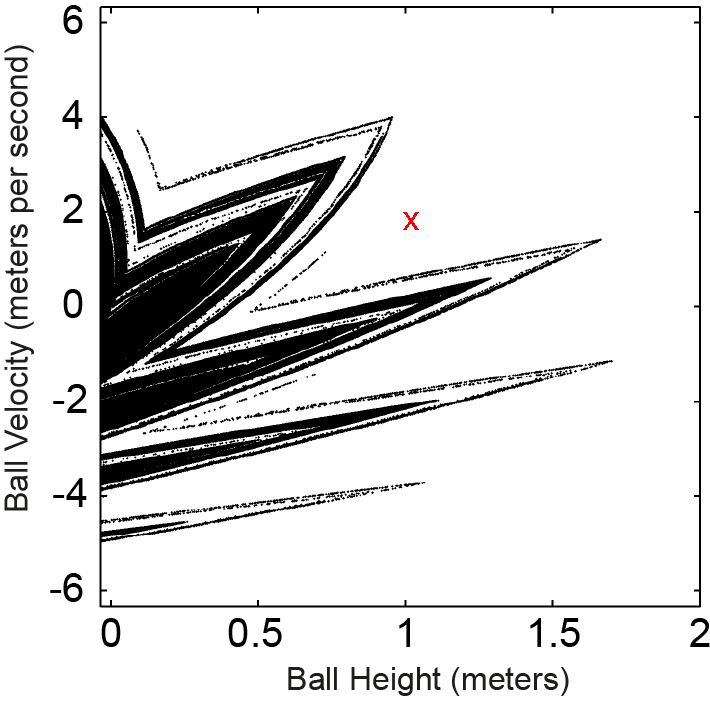
Figure 3
The illustration shows the strange attractor of chaotic ball motions, where each black dot represents a measured ball height and velocity at the paddle’s lowest point (see video). The attractor’s nature causes any ball starting outside the black set, like the red cross, to quickly converge to it, while local instability causes nearby balls on the black set to rapidly diverge.
